Microtonal music is a subject seldom tackled. First, it’s complex and pretty much endless, and then it’s also quite obscure, being only rarely used in day-to-day context. Therefore, it’s often never even encountered to begin with. With this article, I will try to demystify the theory behind microtonal music so you can understand it, and hopefully appreciate it. I will also hop between the terms microtonal and xenharmonic, as they are interchangeable.
First of all, some basics. In music, a note has a pitch and a duration. What’s important, today, is the pitch. Pitch is the height of the note, and can be measured via frequency, in Hertz (Hz). The note to which pretty much all music is attuned to, in the Western world, is A440. This means that the note of A is set to the 440 Hz frequency. It’s also called ‘concert pitch’. Double that frequency and you have the note one octave above, and halve it you get the octave below.
In Western music, the octave is divided into twelve equally-separated notes. It’s important to understand that the notion of ‘equal division’ is not on a straight line, but rather on a logarithmic scale. For example, A5 (880 Hz) has a frequency twice as high as A4 (440 Hz), but four times that of A3 (220 Hz), even though A5 is only two octaves above A3; it will be eight times A2 and sixteen times A1 (and so on). Cents are often used when tuning instruments or when speaking about musical notes because they are based on a logarithmic scale too, which means that there is always the same amount of cents between any two adjacent notes in the twelve tone system, no matter their pitch, and this amount is 100 cents.
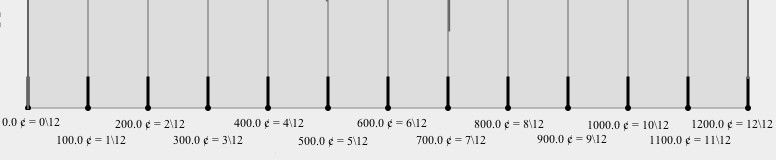
Figure 1. The octave divided in twelve equal parts of 100 cents
In common occidental music — the one I assume you are most familiar with, for the sake of the article — each octave is divided into twelve equal notes. Two notes played at once form an interval, so there are twelve possible intervals in this system (eleven if you don’t count the unison as an interval). In the history of Western music, we’ve come to accept more and more intervals as sounding ‘good’, or judged consonant by at least some part of the listeners. At first, only the unison was deemed good, and this has given us the Gregorian chants, among others. It can be beautiful, but since it consists of a single melodic line, unaccompanied, it can get somewhat underwhelming to our modern ears. As time went on, the perfect fourth and fifth became acceptable and opened a wide range of possibilities to composers of the time. More and more intervals would come, along with newer techniques such as atonal music and twelve-tone serialism.
Today, we have artists like Ron Jarzombek (Blotted Science) who creates wonderful music using the twelve-tone system and Ulcerate, who put an emphasis on dissonance with the use of the minor second interval (one semitone up). These are only two examples, but there are countless others. This is only to say that we’ve reached a time where even the smallest interval possible, the most dissonant one, is judged all right by a considerable portion of music listeners (and that’s without mentioning the long-forbidden tritone).
The time is ripe to go beyond this system. It isn’t to say that microtonal music is only dissonance; quite the contrary. You will see that there is plenty of accessible music that is already written, waiting for you to listen. It’s just that the notion of consonance here is somewhat alien to our perception, desperately conditioned to the standard 12-EDO sound and intervals. Xenharmonic music is full of wonderful and exotic sounds, and I hope to make you see them.

Figure 2. Excerpt from Blotted Science’s ‘Cretaceous Chasm’
with superimposed tone rows.
Microtonal music is everywhere, and is much older than Western music. In short, it’s any music system that isn’t twelve equal divisions of the octave. Many traditional instruments nowadays still have notes outside of what I will now call the ‘common system’ for concision. For example, the Arab music system has twenty-four equal divisions of the octave, and Indian classical music has twelve notes per octave, but with unequal divisions. It’s important to note that, to some, these ‘exotic’ music systems sound totally normal, even if they sound ‘off’ or out of tune to many; it’s just a matter of familiarizing your ear to them. There’s a theoretically endless supply of microtonal systems, but I will describe the big categories with examples and talk more about the most common systems.

First, there is the equal division of the octave (EDO) category. There is an infinite number of these, as there is an infinite number of integers we can cram into one octave, but, according to one source, the human perception would only be able to differentiate two notes down to 5 or 6 cents apart. This leaves us with a maximum of 239 practical microtonal systems that divide the octave in equal parts (but we’ll see later that one can make use of higher-integer scales). That’s a pretty long fall from infinity! The EDO category is, I believe, the most common of the three, if only because of its simplicity.
In 1558, French composer Guillaume Costeley wrote ‘Seigneur Dieu ta pitié‘, in 19 tones per octave. Russian composer Ivan Wyschnegradsky wrote many compositions in 24 notes per octave, during the XX century, where he would use two pianos tuned 50 cents apart (one quarter-tone) to play. Here’s an example. There have been multiple other compositions between the XVI and XX centuries, but recordings of them are quite rare. The 24-EDO system is of particular interest here because the twelve-tone system is still there, inside it.
Listen to Jute Gyte and uSSSy for examples of 24-EDO in modern context. There are also other bands, like Last Sacrament, who used 16-EDO instruments on ‘Enantiodromia‘. Experimental rock/metal band Cryptic Ruse used 13-, 15-, and 23-EDO in the making of ‘Chains of Smoke‘, and then 14, 17, and 23 for the atmospheric doom found on ‘Wasting & Thirsting‘. Ilevens is a new experimental pop band using 22-EDO as their regular tuning system, and it works wonderfully well. Xenharmonic electro music artist Sevish used a nine-note scale based in 313-EDO for his song ‘Desert Island Rain‘. I cannot go without mentioning Dolores Catherino and her contemplative synthesizer music, like this 72-EDO piece. Oh, and I used a 26-EDO scale to translate text into music for a symphonic black metal microtonal album, approaching microtonality with an utilitarian mindset rather than as an artistic choice.
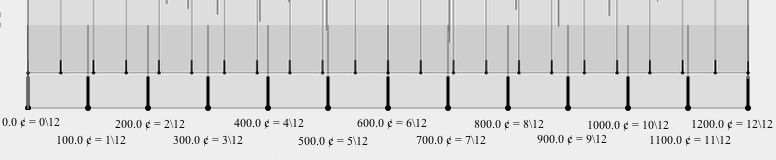
Figure 3. 12-EDO with 22-EDO superimposed.
Let’s have a deeper look at one example, in comparison to the common system, in order to see what one microtonal EDO tuning can bring. For this analysis, I will use the 22-EDO system since the rock band Ilevens uses it extensively and will provide supporting material in the form of quality audio files. First, let’s go through it step by step, literally. Each note, in 22-EDO, is divided by 54.55 cents, making one step almost just like a quarter-tone. However, as you go up the scale, the 4.55 cents difference will add up so that it doesn’t sound like 24-EDO at all anymore. The first four 22-EDO steps fall into the second interval region of the common system, but none of them hit a 12-EDO note perfectly. For that matter, the tritone is the only same interval in the two systems. The fourth one is quite interesting, as it’s a slightly sharp major second (M2), making it sound even brighter. You can click here to listen to the 17:15 ratio, which is a good approximation of this interval.
Then, we get to the four thirds: flat and sharp minors and majors. These can be more tricky to work with, since they are significantly off from common intervals. The subminor third, as you can listen to here, doesn’t sound too foreign, and gives to me the feeling of a more apathetic minor third. The submajor third is a bit flat too, but to a lesser extent, and can almost be used just like a regular one. Moving on, we have two types of fourth. The first one is really close to its 12-EDO cousin, but the other one is more interesting. It’s almost like a major fourth in the 24-tone context. Once again, you can click here and listen to Brendan Byrnes play it and explain what he likes about the interval. After that, we arrive at the tritone, which is the same as in 12-EDO, and the same pattern repeats for the second half of the octave, so I won’t go into further detail, here, just swap the intervals I already mentioned with their upper equivalents. Don’t forget to listen to Brendan Byrnes’ 22-EDO Guitar Étude in full, because it’s absolutely magnificent.

Then, there are just intonation (JI) systems. JI tunings devise their constituent notes according to small number ratios. Therefore, it divides the octave in unequal parts. That’s more attuned to how strings vibrate and how they give off harmonics. For example, a fifth interval is two notes that are 700 cents apart in 12-EDO, but the JI ratio of the pure fifth is 3:2 (or one and a half times the frequency of the first tone), making the JI fifth 702 cents above the tonic. This 2 cent discrepancy is unnoticeable, but others are much more striking. Watch this short video for a comparison of JI and ET (equal temperament) chords.
The twelve-tone system can get the JI treatment and become a microtonal tuning; see this video of Tolgahan Çoğulu to see (and hear!) it in action. Moreover, all scales can be transformed to become justly tuned. But, since JI relies on small number ratios, the amount of possibilities is quite limited. You can choose to raise the higher limit of the integers to any number you imagine, as this threshold is arbitrary, but the nature of JI gets lost the higher you go.
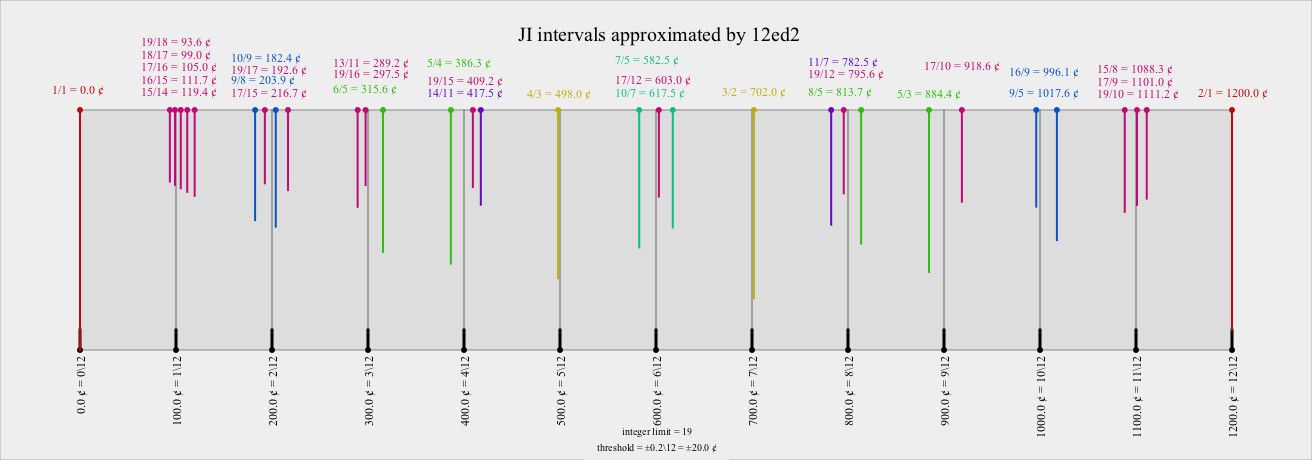
Figure 4. 12-EDO with various JI intervals superimposed (adapted from the Xenharmonic Wiki).
For the analysis of the 12-JI system, I suggest watching (and listening) to this video of the Ultra-Plus guitar. Basically, if you hit all the natural harmonics of a string on your guitar, you get the JI scale, although hitting them all might prove to be quite difficult. Normal fretted guitars will be slightly out of tune with the harmonic series, although providing a decent approximation as well as a lot of convenience. The guitar demonstrated in the video uses 13-limit JI, which means that the ‘small number ratios’ cannot use any prime number higher than 13 (but they can use multiples of that prime number).

Here, we get into weirder territory. Non-octave scales (NOS) are systems that don’t cycle at the 2:1 ratio, commonly known as octave. The most widely-known NOS is the Bohlen-Pierce (BP) scale, conceived in the seventies. Its cycle repeats at the 3:1 ratio, which they call the tritave. In the common system, A3 (220 Hz)’s octave is A4 (440 Hz). However, in the BP scale, its tritave would be 660 Hz, or a slightly sharp E5 in 12-EDO. Then, the notes repeat.
It’s important to understand that each note on a tritave is treated as equivalent as each note on the tritaves above and below, just like how we treat notes on different octaves in the common system. This tritave is then divided into 13 equally divided steps, but they can also be attuned to JI with small integer ratios. As a consequence, each step in BP is bigger than a semitone in 12-EDO. Elaine Walker uses the BP scale in some songs of her experimental pop project ZIA; listen to ‘Stick Men‘ to have an impression of the tuning. Sevish also puts the BP to good use on Callisto.
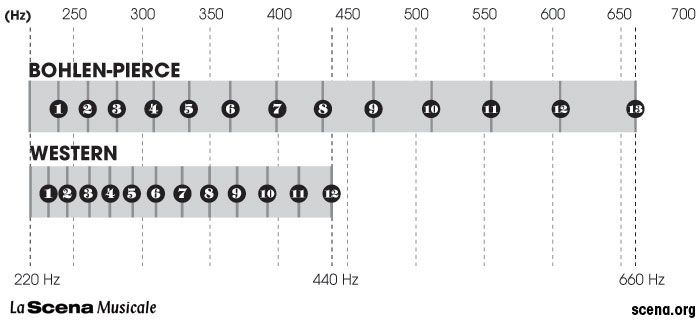
Figure 5. 12-EDO with the Bohlen-Pierce scale superimposed (credit: scena.org)
The Bohlen-Pierce scale is not the only non-octave system out there. In fact, as with most things we see today, there’s an infinite number of NOS you could come up with. However, I will provide one other example. The Harmonic@Dentity-12 (HD12) scale, devised by microtonal musician X.J. Scott, repeats at the 12:7 ratio — slightly bigger than a regular major sixth — and contains ten steps in JI mode. Brendan Byrnes used this crazy tuning (with added half-steps), in songs like ‘Zibra Island‘, and I highly recommend you check the album ‘Micropangaea‘, featuring a wide array of microtonal tunings.
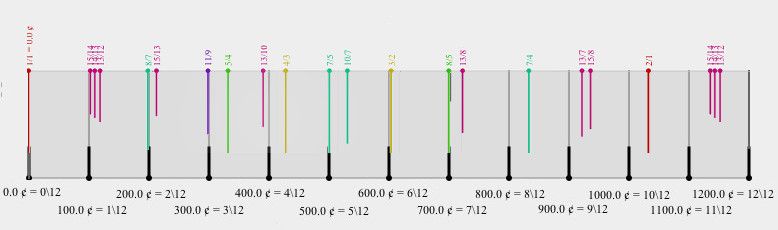
Figure 6. 12-EDO with equal temperament and various possible just intonation intervals
of the Harmonic@Dentity-12 scale superimposed.
The HD12 JI scale (coloured bars) gives a pretty good approximation of the minor and major seconds and minor third while its equal temperament (white thermometers) plays minor and major seconds quite close to the common ones, but grow further apart from the 12-EDO system with each step. The octave of the HD12 scale would sound like a very sharp major sixth. It’s quite unnatural to think of two notes that sound like an out-of-tune major sixth as being an octave, in this system, and thus completely equivalent and interchangeable… But such is the realm of non-octave scales.
Now that we’ve covered some music history and the different categories of microtonal music, let’s talk a little bit about microtonal notation. I won’t go on for too long, here, since, as you will see, it’s complex and inconsistent. Let’s just go over the commonly used notation and accidentals so we’re all on the same page. The notes are classically written on a staff with five lines, each line and interline representing a plain note (A, E, G…) These notes can receive accidentals to represent a sharp (♯), flat (♭), or natural (♮) note. Additionally, there are the double sharp and double flat ones, which must be used in certain circumstances. Now on to microtonal music. There is only a limited number of accidentals widely accepted for microtonal notation. The most common ones are for quarter-tone music (24-EDO). There are the half-flat, one quarter-tone down, and the half-sharp, one quarter-tone up. Alternatively, you could come across a reversed flat symbol instead of the stroked flat. Other than that, there is no microtonal notation system agreed upon that can cover more than one microtonal tuning, and many tunings might have more than one conflicting notation systems. Often, the system will include different symbols, like arrows or numbers, but as the amount of notes per octave in a system goes up, so does the complexity of the suggested notations. I believe one of the next steps in microtonal music will be to create a comprehensive system that can accommodate most, if not all, microtonal tunings. I would personally be in favour of keeping the classical accidentals, but expanding the notation staff depending on your number of notes per octave (or tritave (or other)). This way, the flat and sharp symbols, instead of representing a change of 100 cents, might represent 54.55 cents (22-EDO), 146 cents (Bohlen-Pierce), or a varying value according to the note on the line (just intonation tunings). But that’s just my rough and undeveloped idea…
Now, I’m sure, all this knowledge has you foaming at the mouth. ‘But now‘, you ask, ‘how can we put this into practice?’ Well, let me give you some advice:
First of all, if you’re a musician, I suggest getting a microtonal music notation software like Scala, which is free, or Mus2, which you can try for free. Then, download some free microtonal synthesizer softwares from this list, and try them out with any scale you want; you can find a lot of them on the Xenharmonic wiki. I suggest playing with the same scale for enough time before deciding to move on or not, just to let your ear get used to it. Of course, at first, everything will sound wrong, but with time you’ll see the defining characteristics of the scales and then you can decide if that’s what you want or not.
If you’re not a keyboard player, it can be a bit tougher to begin with microtonal music. Fretless instruments are not too uncommon nor too expensive, but they lack the precision of a fretted one. You can always put fingerboard tapes to help you with a tuning, but it will never be the same as a fretted instrument. Custom-made fretboards and guitars are available too, most notably from Metatonal Music. Then, there’s Tolgahan Çoğulu’s adjustable fret instruments. He can make custom guitar, bass, and other instruments, but I have no idea of the range of price, here. The good thing is that you will have an almost endless number of possibilities with only one instrument.
If you’re more of a listener (musician can be listeners as well), all I can say is to keep an open mind! Learn the personalities of each microtonal tuning system by listening to them as much as possible, and you’ll grow accustomed to them and be able to appreciate them. There are quite a lot of xenharmonic musicians on youtube and facebook, so search for them there. Some good groups I know on facebook would be the Xenharmonic Alliance II and Microtonal Music and Theory. There, you’ll find many microtonal musicians sharing their works, but also listeners that share good or interesting pieces. I’ve added a short list of musicians who make xenharmonic music – exclusively or not -, in an appendix at the end of the article, so I would suggest by starting there. There are many different genres and styles of music, so if black metal is not for you, there’s drum and bass, folk, psychedelic rock, pop, etc. And it’s only a small selection of hand-picked musicians and bands, there are many more out there for you to discover.
In conclusion, you now know a bit more about music, hopefully. Beyond the 12 notes per octave enclave we live in lies an open world only sparsely populated in comparison, with fertile soil waiting to be cultivated and bear fruits. Microtonal music is not a mysterious thing, it’s just woefully underexploited and misunderstood. If this article has given you the taste to search and appreciate microtonal music by yourself, I will have accomplished my mission. If it has given you the desire to create some, then share the results with us!
…
Appendix: A selection of microtonal artists
Aaron Myers-Brooks (24-EDO)
Amogh Symphony (multiple tunings)
Aphex Twin (multiple tunings)
Beyond the Event Horizon (unknown)
Brendan Byrnes (multiple tunings)
Cryptic Ruse (multiple tunings)
Dolores Catherino (multiple tunings)
Holy Palms (24-EDO)
Ilevens (22-EDO)
Ivan Wyschnegradsky (24-EDO)
Jute Gyte (24-EDO)
Last Sacrament (16-EDO)
Melopœia (multiple tunings)
The Mercury Tree (multiple tunings and 12-EDO)
Pilot (Turkish music)
Redrick Sultan (19-EDO)
Sevish (multiple tunings)
Tolgahan Çoğulu (multiple traditional tunings)
ZIA (multiple tunings)